Module 02
Finite state spaces and combinatorics
TC and DJM
Last modified — 24 Feb 2026
1 Induced probabilities in “obvious” cases
Finite Sample Spaces
In some cases, the sample space contains finite number of possible outcomes, and they are equally likely (they should receive equal probabilities).
Example
- Experiment: roll a fair die;
- Sample space: \(\Omega = \{1, 2, 3, 4, 5, 6\}\).
- If the die is fair we have \[\mathbb{P}(\{1\}) = \mathbb{P}(\{2\}) = \cdots = \mathbb{P}(\{6\})\]
Finite and equally likely outcomes
When there are finitely many outcomes, and they are equal likely, calculating probabilities involves counting outcomes in events/sets, which can be challenging
This module goes over some generic counting techniques, which can be used to calculate probabilities.
Equally likely outcomes
Let \(A\) be a subset (event) of a sample space \(\Omega\).
\[ \mathbb{P}\left( A\right) = \frac{\text{number of elements in }A}{\text{number of elements in }\Omega } \]
Basic principle
Suppose that a random experiment has 2 steps, where
- Step 1 has \(n_1\) possible outcomes, and
- Step 2 has \(n_2\) possible outcomes.
Then, \[\mbox{total number of possible outcomes} \ = \ n_1 \times n_2\]
We are implicitly assuming that the outcome of the second step does not depend on the outcome of the first step.
Extension to “k-step” experiments
If a random experiment has k steps.
- Step 1 has \(n_1\) possible outcomes,
- Step 2 has \(n_2\) possible outcomes,
\(\quad\quad\quad\vdots\quad\quad\quad\)
- Step k has \(n_k\) possible outcomes.
Then, \[\mbox{total number of outcomes} \ = \ n_1 \times n_2 \times n_3 \times \cdots \times n_k\]
Note
Implicit assumption: the outcomes of each step do not depend on each other.
License Plates
Exercise 1
How many different license plates with 7 characters are possible if the first 3 places are letters and the last 4 are numbers?
How many different license plates are there with no repeated letters or numbers?
What is the probability that a randomly chosen license plate has no repeats?
2 Permutations
Permutation
Definition
Example
- Some permutations of the elements of A are:
\[\left( 3, 5, 2, 4, 1 \right), \, \left( 2, 1, 3, 4, 5 \right), \, \left( 5, 4, 2, 1, 3 \right), \quad \mbox{ etc.} \]
- Those are all different permutations:
\[\left( 2, 1, 3, 4, 5 \right) \quad \neq \quad \left( 1, 2, 3, 4, 5 \right) \quad \neq \quad \left( 1, 3, 2, 4, 5 \right)\]
Counting permutations
Exercise 2
Counting permutations
Convention
Recall that we define \(0!=1\). This makes \(26! = 26!\times 0!\) and \(15! / 0! =15!\).
Key assumption in counting permutations this way:
all \(n\) objects are distinct.
When some of them are not distinct, the number of possible distinct outcomes by re-arrangement (“permutation”) is not given by this formula.
We need a different formula.
Example
In how many different ways can the letters of “pepper” be arranged? Answer:
- If the letters were all different, we would have \(6!=720\) arrangements.
- But each arrangement does not change if:
- we permute the 3 p’s (3! ways of doing this)
- we permute the 2 e’s (2! ways of doing this)
- Thus, in the list of 6! arrangements, each “p/e” pattern appears \(3! \times 2!\) times: \[\text{number of arrangements}=\frac{6!}{3!2!}=60.\]
International chess
A chess tournament with 10 players:
| # of players | Country of origin |
|---|---|
| 4 | Russia |
| 3 | USA |
| 2 | Canada |
| 1 | Brazil |
Exercise 3: Counting outcomes
- If we see only nationalities in the final rank, how many outcomes are possible?
- If all players have an equal chance to win, what is the probability that Canada wins the tournament?
Wedding Seating
Exercise 4
Eight wedding guests (A, B, C, D, E, F, G, H) need to be seated next to each other in a line. Unfortunately, A and B don’t like each other very much.
- How many ways are there to seat the guests such that A and B don’t sit next to each other?
- How does the answer change if the table is circular (not a line)?
- How does the answer change if the table is circular and the seats are not distinguishable?
3 Combinations
Combinations
Definition
Consider the set \[S=\left\{ a, b, c, d, e\right\}\]
The following are all the possible subsets of \(S\) of size 3:
| \(\{ a, b, c\}\) | \(\left\{ a, d, e\right\}\) |
| \(\{ a, b, d\}\) | \(\left\{ b, c, d\right\}\) |
| \(\{ a, b, e\}\) | \(\left\{ b, c, e\right\}\) |
| \(\{ a, c, d\}\) | \(\left\{ b, d, e\right\}\) |
| \(\{ a, c, e\}\) | \(\left\{ c, d, e\right\}\) |
- We call these sets “combinations” when we only care which elements are in the set.
Combinations
- Note that the order of the elements does not matter (these are sets, not sequences).
\[\Bigl\{ a, b, d \Bigr\} \, = \, \Bigl\{ d, a, b \Bigr\} \, = \, \Bigl\{ b, d, a \Bigr\} \] (and other possible rearrangements).
- Given a set of \(n\) distinct items \[S = \{s_1,\ s_2,\ \dots, s_n\}\] how many different combinations of size \(m\) can be formed? (where, of course, \(m \le n\))
Number of combinations
The number of combinations of size \(m\) out of a set of size \(n \ge m\) has various notations:
\[\binom{n}{m} = \left._{n} C_{m}\right. = C_m^n\]
- \(n\): size of the set from which combinations are drawn
- \(m\): size of the combinations
- we read it as “n choose m”
Tip
In this course we use \(\binom{n}{m}\).
Example
For example, when \(n=5\) and \(m=3\) we have
| \(\{ 1,2,3\}\) | \(\left\{ 1,4,5\right\}\) |
| \(\{ 1,2,4\}\) | \(\left\{ 2,3,4\right\}\) |
| \(\{ 1,2,5\}\) | \(\left\{ 2,3,5\right\}\) |
| \(\{ 1,3,4\}\) | \(\left\{ 2,4,5\right\}\) |
| \(\{ 1,3,5\}\) | \(\left\{ 3,4,5\right\}\) |
hence, the number of combinations must be
\[\binom{5}{3}= {10}\]
General formula
\[\binom{n}{m} = \frac{n!}{m!(n-m)!}\]
These are also called binomial coefficients.
They have many beautiful interpretations.

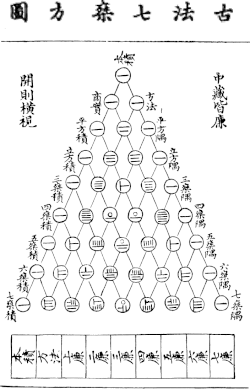
Prove the general formula
Exercise 5
\[\binom{n}{m} = \frac{n!}{m!(n-m)!}.\]
Hint: remember that \(0! = 1\).
Lotto 6/49
Dealer secretly chooses 6 distinct integers between 0 and 49.
Player randomly selects 6 distinct integers between 0 and 49.
The more matches, the bigger the prize.
Exercise 6
Building a Committee
- A club has 12 members.
- A committee of 4 members (president, vice-president, and 2 secretaries with identical roles) is to be formed.
Exercise 7
- Solve the problem by formulating it as a k-step experiment.
- Solve the problem by formulating it as a choice of 4 members, and then a permutation to assign them to roles.
Do the answers align?
Making a Password
You need to construct a 8-character password out of lowercase letters (a-z) and numbers (0-9).
Exercise 8
Combination Symmetry
Exercise 9
- Show that \({n\choose k} = {n\choose n-k}\)
- Show that \({n\choose k+1} \geq {n\choose k}\) if and only if \(n-k \geq k+1\)
- Argue that \({n\choose k}\) is maximized at \(k = \lfloor \frac{n-1}{2}\rfloor + 1\). In other words, the number of combinations is largest when \(k \approx n/2\).
Stat 302 - Winter 2025/26