00 Review and bonus clickers
Stat 406
Geoff Pleiss, Trevor Campbell
Last modified – 04 December 2024
\[ \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\minimize}{minimize} \DeclareMathOperator*{\maximize}{maximize} \DeclareMathOperator*{\find}{find} \DeclareMathOperator{\st}{subject\,\,to} \newcommand{\E}{E} \newcommand{\Expect}[1]{\E\left[ #1 \right]} \newcommand{\Var}[1]{\mathrm{Var}\left[ #1 \right]} \newcommand{\Cov}[2]{\mathrm{Cov}\left[#1,\ #2\right]} \newcommand{\given}{\ \vert\ } \newcommand{\X}{\mathbf{X}} \newcommand{\x}{\mathbf{x}} \newcommand{\y}{\mathbf{y}} \newcommand{\P}{\mathcal{P}} \newcommand{\R}{\mathbb{R}} \newcommand{\norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\snorm}[1]{\lVert #1 \rVert} \newcommand{\tr}[1]{\mbox{tr}(#1)} \newcommand{\brt}{\widehat{\beta}^R_{s}} \newcommand{\brl}{\widehat{\beta}^R_{\lambda}} \newcommand{\bls}{\widehat{\beta}_{ols}} \newcommand{\blt}{\widehat{\beta}^L_{s}} \newcommand{\bll}{\widehat{\beta}^L_{\lambda}} \newcommand{\U}{\mathbf{U}} \newcommand{\D}{\mathbf{D}} \newcommand{\V}{\mathbf{V}} \]
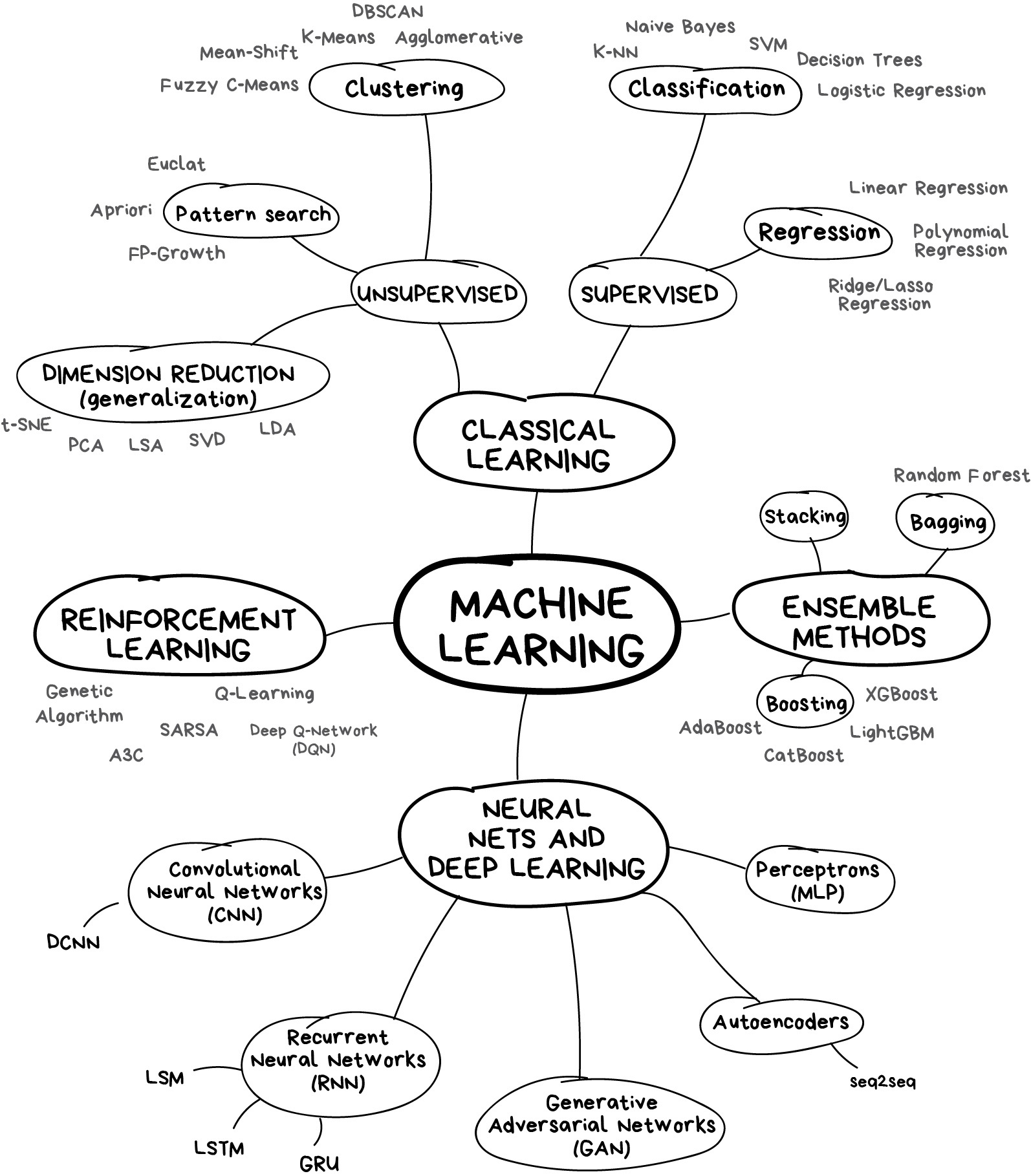
Big picture
- What is a model?
- How do we evaluate models?
- How do we decide which models to use?
- How do we improve models?
General stuff
- Linear algebra (SVD, matrix multiplication, matrix properties, etc.)
- Optimization (derivitive + set to 0, gradient descent, Newton’s method, etc.)
- Probability (conditional probability, Bayes rule, etc.)
- Statistics (likelihood, MLE, confidence intervals, etc.)
1. Model selection
- What is a statistical model?
- What is the difference between training error, test error, and risk?
- What is the (theoretical) predictor with the lowest risk for regression? For classification?
- Why can we not obtain these predictor in practice?
- What is the bias-variance tradeoff?
- What is the goal of model selection?
- What is the difference between AIC / BIC / CV / Held-out validation?
2. Regression
- What do we mean by regression?
- What is regularization?
- What is the goal of regularization?
- What is the difference between L1 and L2 regularization?
- How do we do non-linear regression?
- What are splies?
- What are kernel smoothers?
- What is knn?
- What are decision trees?
- What is the curse of dimensionality?
3. Classification
- What is classification?
- What is the difference between a generative versus descriminative classification model?
- What is a decision boundary? When is it linear?
- Compare logistic regression to discriminant analysis.
- What are the assumptions made by each method?
- What are the shapes of the decision boundaries?
- What are the positives and negatives of trees?
- How do we measure performance of classification beyond 0-1 loss?
- What is a probabilistic notion of classification performance?
- How do we measure the goodness of uncertainty estimates?
4. Modern methods
- What is the bootstrap?
- What is the difference between bagging and boosting?
- When do we prefer one over the other (think bias-variance tradeoff)?
- What is the difference between random forests and bagging?
- How do we understand Neural Networks?
- What is the difference between neural networks and other non-linear methods?
- What is the difference between increasing width and increasing depth? (Number of parameters, expressivity)
- How do we train neural networks? What is backpropagation?
- Why are we surprised that neural networks “work”?
5. Unsupervised learning
- What is unsupervised learning?
- What is dimensionality reduction?
- What is the difference between PCA vs KPCA?
- What do the principle components represent?
- What is clustering?
- What is the difference between k-means and hierarchical clustering?
Pause for course evals
Currently at 51/144.
A few clicker questions
The singular value decomposition applies to any matrix.
- True
- False
Which of the following is true about the training error?
- It will decrease as we add interaction terms
- It will decrease as we add more training data
- It will decrease as we add more regularization
- It will decrease as we remove useless predictors
(Multiple answer)
Which of the following is an advantage to using LOO-CV over k-fold CV?
- The bias of LOO-CV, as a risk estimator, is lower than that of k-fold CV.
- The variance of LOO-CV, as a risk estimator, is lower than that of k-fold CV.
- It can be computed more quickly than k-fold CV for kernel smoothers.
- It can be computed more quickly than k-fold CV for ridge regression.
(Multiple answer)
Which of the following reduce the bias of linear regression?
- Adding a ridge penalty
- Adding a lasso penalty
- Adding interaction terms / nonlinear basis functions
- Adding more training data
(multiple answer)
The decision boundary for classification problems…
- Is the set of points where \(P(Y=1|X) = P(Y=0|X)\)
- Is the set of points where \(P(Y=1|X) / P(Y=0|X) = P(Y=1) / P(Y=0)\)
- Is the set of points where \(P(Y=1|X) / P(Y=0|X) = P(Y=0) / P(Y=1)\)
- Is linear for all discriminant analysis predictors
(multiple answer)
Which of the following properties of boosting are true?
- The risk can be estimated without a holdout set
- The component predictors can be trained in parallel
- The predictive uncertainty can be estimated by the variance of the predictors
- The bias of the ensemble is lower than the bias of the component predictors
- The variance of the ensemble is lower than the variance of the component predictors
(multiple answer)
Which of the following statements are true about PCA and KPCA?
- PCA requires specifying the number of principled components, while KPCA does not
- KPCA requires the data to be centered, while PCA does not
- PCA is a linear method, while KPCA is a non-linear method
- After performing KPCA, the principle components can be used to reduce the dimensionality of new (previously unseen) test data
UBC Stat 406 - 2024