class: center, middle, inverse, title-slide # 02 Convex sets and functions ### STAT 535A ### Daniel J. McDonald ### Last modified - 2021-01-13 --- ## Some history `$$\newcommand{\E}{\mathbb{E}} \newcommand{\Expect}[1]{\mathbb{E}\left[ #1 \right]} \newcommand{\Var}[1]{\mathbb{V}\left[ #1 \right]} \newcommand{\Cov}[2]{\mathrm{Cov}\left[#1,\ #2\right]} \newcommand{\given}{\ \vert\ } \renewcommand{\P}{\mathbb{P}} \newcommand{\R}{\mathbb{R}} \newcommand{\argmin}[1]{\underset{#1}{\textrm{argmin}}} \newcommand{\F}{\mathcal{F}} \newcommand{\norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\indicator}{\mathbb{1}} \renewcommand{\bar}{\overline} \renewcommand{\hat}{\widehat} \newcommand{\tr}[1]{\mbox{tr}(#1)} \newcommand{\X}{\mathbb{X}} \newcommand{\Set}[1]{\left\{#1\right\}} \newcommand{\dom}[1]{\textrm{dom}\left(#1\right)} \newcommand{\st}{\;\;\textrm{ s.t. }\;\;}$$` * Historically, linear problems were the focus * Linear vs. non-linear guided the discussion * The more appropriate distinction is between **convex** and **non-convex** * Why? Because with "convex problems", local minima are global minima .center[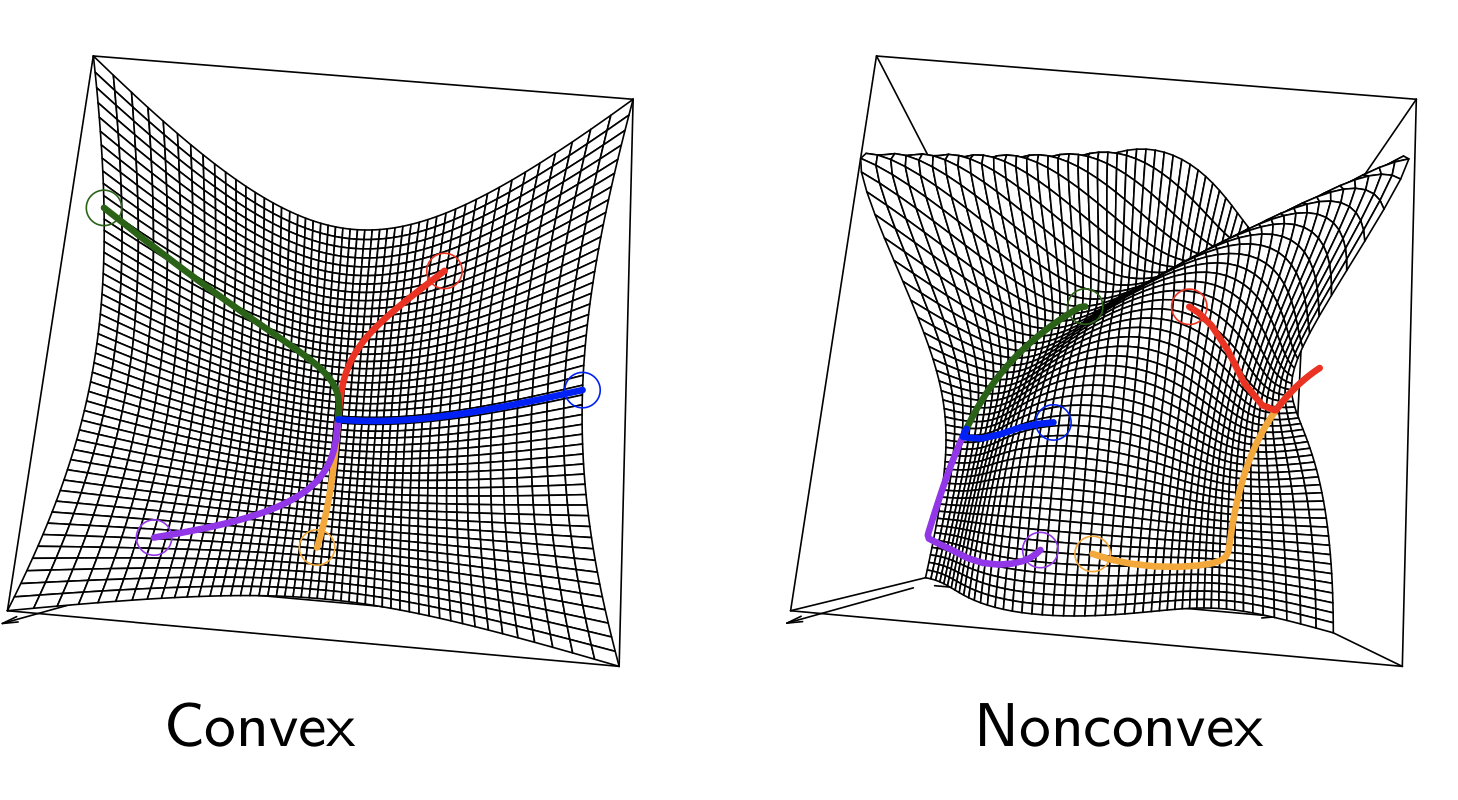] --- ## Topics today 1. Convex sets and operations preserving them 2. Convex functions and operations preserving them 3. Practice --- ## Definitions Set `\(C\)` is **convex** iff `\(\forall \ x,y \ \in C, \forall t \in [0,\ 1]\ \ t x + (1-t) y \in C.\)` So `\(C\)` is convex iff for any two points in `\(C\)` the segment connecting them is also entirely in `\(C\)`. .pull-left[ .center[  ]] .pull-right[.center[  ]] **Convex combination** of set of points `\(x_1, \ldots, x_k \in \mathbb{R}^n\)` is `$$\Set{\sum\limits_{i=1}^{k} \theta_i x_i : \sum\limits_{i=1}^{k} \theta_i=1,\ \forall i\ \theta_i \in [0,\ 1]}.$$` **Convex hull** of any `\(C \in \mathbb{R}^n\)`, denoted `\(conv(C)\)` is a union of all convex combinations of different elements of `\(C\)`. --- ## Some examples - Trivial: Empty set, point, line, segment. - Norm ball: `\(\Set{x : \left\lVert x \right\rVert < r}\)`. - Hyperplane `\(\Set{x : {a}^\top x = b}\)`, Affine space `\(\Set{x : A x = b}\)`. - Hyperspace: `\(\Set{x : {a}^\top x \leq b}\)`, Polyhedron `\(\Set{x : A x \leq b}\)`. - Cone such that if `\(x_1, x_2 \in C\)` then `\(t_1 x_1 + t_2 x_2 \in C \ \forall \ t_1, t_2 \geq 0\)`. --- ## Cones Set `\(C\)` is a **cone** iff `\(\forall\)` scalars `\(t \geq 0\)`, `\(x \in C \implies t x \in C\)`. .center[  ] Type of cones: * Norm cone: `\(\Set{(x,a),\ x \in R^p,\ a \geq 0: \left\lVert x \right\rVert \leq a}\)`. * Normal cone for some `\(C\)` and `\(x \in C\)`: `\(N_C(x) = \Set{g : {g}^\top x \geq {g}^\top y \ \forall \ y \in C}\)`. * Positive semidefinite cone `\(\mathcal{S}_+^n = \Set{X \in \mathcal{S}^n : X \succeq 0}\)`, `\(\mathcal{S}^n\)` is the set of symmetric matrices. -- Are all cones convex? --- **Normal cone**: for some `\(C\)` and `\(x \in C\)`: `$$N_C(x) = \Set{g : {g}^\top x \geq {g}^\top y \ \forall y \in C}$$` Always convex, regardless of `\(C\)` .center[  ] --- ## Key properties of convex sets **Separating hyperplane.** `\(A, B\)` are convex, nonempty, disjoint sets. Then `$$\exists a,b:\ A \subseteq \Set{x : {a}^\top x \leq b},\ \ B \subseteq \Set{x : {a}^\top \geq b}$$` .pull-left[ .center[  ]] .pull-right[.center[  ]] --- **Supporting hyperplane.** .pull-left[ `\(C\)` nonempty, convex, `\(x_0 \in bd(C)\)`. .center[  ]] .pull-right[.center[ Then `\(\exists a:\ C \subseteq \Set{x : {a}^\top x \leq {a}^\top x_0}\)`  ]] -- .center[  ] --- ## Operations preserving convexity - **Intersection**. `\(A\)` and `\(B\)` convex `\(\Longrightarrow C = A \cap B\)` convex - **Scaling, translation**. `\(C\)` is convex `\(\implies a C + b\)` is convex. - **Affine image and preimage**. `\(f(x) = A x + b\)`, `\(C\)` is convex `\(\implies f(C),\ f^{-1}(C)\)` are convex. - Lots more, see BV chapter 2. --- ## Example The perspective function applied to a convex set: `\(f_z: \R^n \rightarrow \R^n\)` where `\(f_z (x) = x/z\)` and `\(z \in \R,\ z>0\)`. If `\(C\)` is convex, then `\(D = f_z(C)\)` is. If `\(D\)` is convex, then `\(C=f_z^{-1}(D)\)` is. --- Consider `\(U,V\)` discrete random variables with support `\(\Set{1,\ldots,m}\)` and `\(\Set{1,\ldots,n}\)`. Let `\(C\)` be a set of joint distributions: * `\(\forall p \in C\)`, `\(p_{ij} = P(U=i,\ V=j)\)`, * length of `\(p\)` is `\(n\times m\)`, * `\(p_{ij} \in [0,1]\)`, `\(\sum p_{ij} = 1\)`. Let `\(D\)` be the set of conditional distributions: `\(\forall q \in D\)`, `\(q_{ij} = P(U=i\ |\ V=j)\)`. Assume `\(C\)` is a convex set. Is `\(D\)`? -- `$$q_{ij} = \frac{p_{ij}}{\sum_{k=1}^n p_{kj} } \Rightarrow q=\frac{p}{a^\top p}$$` This is the perspective function composed with an affine function. So `\(D\)` is convex if `\(C\)` is. --- ## Convex functions Function `\(f: \mathbb{R}^n\to \mathbb{R}\)` is **convex** iff `\(\dom{f} \subseteq \mathbb{R}^n\)` is convex and `$$\forall x,y \in \dom{f}, t \in [0,\ 1] \ \ \ f(t x + (1-t) y) \leq t f(x) + (1-t) f(y)$$` <img src="rmd_gfx/02-convexity/convex-fun-1.svg" style="display: block; margin: auto;" /> * `\(f\)` lies "below" the segment joining `\(f(x)\)` and `\(f(y)\)` * **Concave** is the opposite .center[ `\(f\)` concave `\(\Rightarrow\)` `\(-f\)` convex ] --- ## Modifiers `\(f\)` is **strictly convex** iff `\(\forall t \in (0,\ 1),\ \forall x \neq y\)` the inequality is strict. * `\(f\)` linear, then it is convex (and concave). * `\(f\)` strictly convex, then it is "more" convex than a line is `\(f\)` is **strongly convex** with parameter `\(\tau\)` iff `\(f(x) - \frac \tau 2 \left\lVert x \right\rVert_2^2\)` is convex. * `\(f\)` is at least as convex as a quadratic Strong `\(\Rightarrow\)` Strict `\(\Rightarrow\)` Convex Same for concave --- ## Examples - `\(f(x) = \frac 1 x\)` for `\(x \in (0,\infty)\)` is strictly convex, but not strongly. - Univariate functions: - `\(e^{ax}\)` is convex `\(\forall a \in \mathbb{R}\)` over `\(\mathbb{R}\)`. - `\(x^a\)` convex given `\(a \geq 1\)` or `\(a \leq 0\)` over `\(\mathbb{R}_+\)`. - `\(\log x\)` is concave over `\(\mathbb{R}_+\)`. - Affine `\({a}^\top x + b\)` is both convex and concave. - Quadratic `\(\frac 1 2 {x}^\top Q x + {b}^\top x + c\)` is convex if `\(Q \succeq 0\)`. --- - `\(\left\lVert u - A x \right\rVert_2^2\)` convex since `\({A}^\top A \succeq 0\)`. - Norms: all vector norms and most matrix norms (Schatten norms, induced norms) are convex. - `\(\norm{x}_q\)` `\(0 \leq q < 1\)` is not convex - Indicator function is convex. `\(C\)` is a convex set, then `$$I_C(x) = \begin{cases} 0 & x \in C \\ \infty & \mbox{otherwise} \end{cases}$$` - Support function is convex for any set `\(C\)`. `$$I_C^*(x) = \max\limits_{y \in C} {x}^\top y$$` --- ## Key properties - `\(f\)` is convex iff its restriction to any line is convex - `\(f\)` is convex iff its **epigraph** is convex, where `$$\textrm{epi}(f) = \Set{ (x,t) \in \dom{f} \times \R : f(x) \leq t}$$`. <img src="rmd_gfx/02-convexity/epigraph-1.svg" style="display: block; margin: auto;" /> - `\(f\)` is convex `\(\implies\)` all its sublevel sets are convex. `\(C_t = \Set{x \in \dom{f} : f(x) \leq t}\)`. The converse is false. --- The definition `$$\forall x,y \in \dom{f}, t \in [0,\ 1] \ \ \ f(t x + (1-t) y) \leq t f(x) + (1-t) f(y))$$` is sometimes called **zeroth-order** definition **First order** characterization: if `\(f\)` is differentiable, then `\(f\)` is convex iff `\(\dom f\)` is convex and `$$\forall x,y \in \dom{f}\ \ f(y) \geq f(x) + \nabla {f(x)}^\top (y-x)$$` Essentially, it means that `\(f\)`'s graph lies above any tangent plane. Note the implication: if `\(f\)` is differentiable, then `\(\nabla f(x) = 0 \Rightarrow x\)` minimizes `\(f\)` **Second order** characterization: if `\(f\)` is twice differentiable, then `\(f\)` is convex iff `\(\dom{f}\)` is convex and `$$\forall x \in \dom{f}\ \ \nabla^2 f(x) \succeq 0$$` --- ## Operations preserving function convexity Nonnegative linear combination. Pointwise maximum. `\(\forall s \in S\ \ f_s\)` is convex `\(\implies f(x) = \max_{s \in S} f_s(x)\)` is also convex. Partial minimum. If `\(g(x,y)\)` is convex over variables `\(x, y\)` and `\(C\)` is convex, then `\(f(x) = \min\limits_{y \in C} g(x,y)\)` is also convex. -- Example (distance to a set) **Maximum** Let `\(C\)` be a set (arbitrary), `\(\norm{\cdot}\)` be a norm `$$f(x) = \max_{y\in C} \norm{x-y}$$` **Minimum** Assume `\(C\)` convex, `$$f(x) = \min_{y\in C} \norm{x-y}$$` --- ## Composition **Affine**: `\(f\)` convex implies `\(g(x) = f(Ax + b)\)` convex **General**: `\(g : \R^n\rightarrow\R\)`, `\(h: \R\rightarrow\R\)`, `\(f = h\circ g\)` Remember chain rule: `$$f''(x) = h''(g(x))g'(x)^2 + h'(g(x))g''(x)$$` `\(f\)` convex if * `\(h\)` convex nondecreasing and `\(g\)` convex * `\(h\)` convex nonincreasing and `\(g\)` concave Similar argument for vector composition --- ## Wrap up * Convexity means local==global, it's good * Convex sets: `\(x,y \in C \Rightarrow tx + (1-t)y \in C\)` * Convex functions: domain convex and "function lies below a line" * 0th/1st/2nd-order characterizations * Various ways common operations retain convexity (affine transforms, maximum, minimum, etc.)