04 Gradient descent

class: center, middle, inverse, title-slide

# 04 Gradient descent
### STAT 535A
### Daniel J. McDonald
### Last modified - 2021-01-20

---

## Last time

$$
\newcommand{\R}{\mathbb{R}}
\newcommand{\argmin}[1]{\underset{#1}{\textrm{argmin}}}
\newcommand{\norm}[1]{\left\lVert #1 \right\rVert}
\newcommand{\indicator}{1}
\renewcommand{\bar}{\overline}
\renewcommand{\hat}{\widehat}
\newcommand{\tr}[1]{\mbox{tr}(#1)}
\newcommand{\Set}[1]{\left\{#1\right\}}
\newcommand{\dom}[1]{\textrm{dom}\left(#1\right)}
\newcommand{\st}{\;\;\textrm{ s.t. }\;\;}
$$

.pull-left[
A convex optimization problem 
$$
`\begin{aligned}
\min\limits_{x \in D} &\quad f(x) \\
\text{subject to} &\quad g_i(x) \leq 0 & \forall i \in 1,\ldots, m \\
&\quad A x = b 
\end{aligned}`
$$
where `$f, g_i$` are convex and `$D = \dom{f} \cap \dom{g_i}$`.

]

.pull-left[

* Saw transformations.

* First Order Condition (FOC)

]

.pull-right[

**Relations**

.center[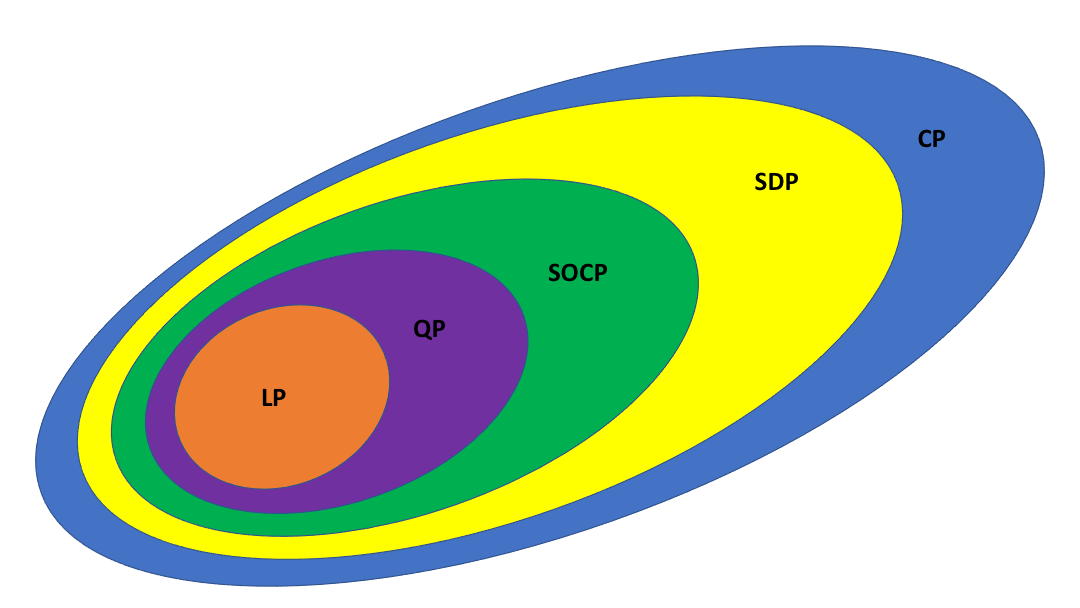
![:scale 80%](gfx/cp-hierarchy.png)
]

]

---

## Very basic example

.pull-left[
Suppose I want to minimize `$f(x)=(x-6)^2$` numerically.

I start at a point (say `$x^{(0)}=23$`)

I want to "go" in the negative direction of the gradient.

The gradient (at `$x^{(0)}=23$`) is  
`$f'(23)=2(23-6)=34$`.

OK go that way by some small amount:

`$x^{(1)} = x^{(0)} - \gamma 34$`, for `$\gamma$` small.

In general, `$x^{(k+1)} = x^{(k)} -\gamma f'(x^{(k)})$`.

]
  
.pull-right[

```r
niter = 10
gam = 0.1
x = double(niter)
x[1] = 23
grad <- function(x) 2*(x-6)
for(i in 2:niter) x[i] = x[i-1] - gam*grad(x[i-1])
```

<img src="rmd_gfx/04-gradient-descent/unnamed-chunk-2-1.svg" style="display: block; margin: auto;" />
]

---

## Today

1. Gradient descent implementation

2. Techniques for increasing speed of convergence

3. What if `$f$` isn't differentiable?

---

## First order methods

For simplicity, consider unconstrained optimization 
`\begin{equation}
\min_x f(x)
\end{equation}`
assume `$f$` is convex and differentiable

__Gradient descent__

-   Choose `$x^{(0)}$`

-   Iterate `$x^{(k)} = x^{(k-1)} - \gamma_k\nabla f(x^{(k-1)})$`

-   Stop sometime

---

## Why does this work?

__Heuristic interpretation:__

* Gradient tells me the slope.

* negative gradient points toward the minimum

* go that way, but not too far (or we'll miss it)

__More rigorous interpretation:__

- Taylor expansion
$$
f(x) \approx f(x_0) + \nabla f(x_0)^{\top}(x-x_0) + \frac{1}{2}(x-x_0)^\top H(x_0) (x-x_0)
$$
- replace `$H$` with `$\gamma^{-1} I$`

- minimize the quadratic approximation in `$x$`:
$$
0\overset{\textrm{set}}{=}\nabla f(x_0) + \frac{1}{\gamma}(x-x_0) \Longrightarrow x = x_0 - \gamma \nabla f(x_0)
$$

---

## Visually

---

## What `$\gamma$`?

What to use for `$\gamma_k$`?

__Fixed__

- Only works if `$\gamma$` is exactly right 
- Usually does not work

__Sequence__

`$$\gamma_k \quad \st \sum_{k=1}^{\infty} \gamma_k = \infty ,\quad
              \sum_{k=1}^{\infty} \gamma^{2}_k < \infty$$`

__Exact line search__

- Tells you exactly how far you want to go
- At each `$k$`, solve
$$\gamma = \arg\min_{s \geq 0} f\big( x^{(k)} - s f(x^{(k-1)})\big) $$
- Usually can't solve this.

---

## Backtracking line search

Approximation to exact line search

1. Set `$0 <\beta < 1 , 0 < \alpha \leq\frac{1}{2}$`

2. At each `$k$`, set `$\gamma=\gamma_0$`. While
`$$f\left(x^{(k)} - \gamma \nabla f(x^{(k)})\right) > f(x^{(k)}) - \alpha \gamma \norm{ \nabla f(x^{(k)})}^{2}_{2}$$`
set `$\gamma \leftarrow \beta \gamma$`

3. `$x^{(k+1)} = x^{(k)} - \gamma \nabla f(x^{(k})$`

---

$$ f(x_1,x_2) = x_1^2 + 0.5x_2^2$$

---

```r
x <- matrix(0,40,2)
x[1,] <- c(1,1)
grad <- function(x) c(2, 1) * x
gamma <- .1
for (k in 2:40) x[k,] <- x[k-1,] - gamma * grad(x[k-1,])
```

---

```r
x <- matrix(0,40,2)
x[1,] <- c(1,1)
gamma <- .9
for (k in 2:40) x[k,] <- x[k-1,] - gamma * grad(x[k-1,])
```

---

```r
x <- matrix(0,40,2)
x[1,] <- c(1,1)
gamma <- .5
for (k in 2:40) x[k,] = x[k-1,] - gamma / sqrt(k) * grad( x[k-1,])
```

---

.pull-left[

```r
fb <- function(x) drop(c(1,0.5) %*% x^2)
gamma0 <- .9
alpha <- 0.5
beta <- 0.9
backtrack <- TRUE
for (k in 2:40) {
  gamma <- gamma0
  gg <- grad(x[k - 1, ])
  while (backtrack) {
    gamma <- beta * gamma
    prop <- x[k-1,] - gamma * gg
    backtrack <- (fb(prop) > fb(x[k-1,]) - 
        alpha * gamma * sum(gg^2))
  }
  x[i,] <- prop
  backtrack <- TRUE
}
```
]

.pull-right[

]

---

## Convergence properties

If `$\nabla f$` is Lipschitz, use fixed `$\gamma$`

1. GD converges at rate `$O(1/k)$`
2. `$\epsilon$`-optimal in `$O(1/\epsilon)$` iterations

If `$f$` is strongly convex as well

1. GD converges at rate `$O(c^k)$` `$(0<c<1)$`.
2. `$\epsilon$`-optimal in `$O(\log(1/\epsilon))$` iterations

We call this second case "linear convergence" because it's linear on the `$\log$` scale.

---

## Momentum

Carry along some information from the previous iterate, (usually `$\eta=0.9$`)

.pull-left[

`$v \leftarrow \eta v + \gamma \nabla f(x^{(k)})$`

`$x^{(k+1)} \leftarrow x^{(k)} - v$`

```r
x[1,] <- c(1,1)
gamma <- .2
eta <- .9
v <- c(0,0)
for (i in 2:40) {
  v <- eta * v + gamma * grad(x[i-1,])
  x[i,] <- x[i-1,] - v
}
```

]

.pull-right[

<img src="rmd_gfx/04-gradient-descent/unnamed-chunk-14-1.svg" style="display: block; margin: auto;" />
]

---

## Nesterov's version (sometimes called "acceleration")

Idea is to let the gradient depend on the momentum as well

.pull-left[

`$v \leftarrow \eta v + \gamma \nabla f(x^{(k)}-\gamma v)$`

`$x^{(k+1)} \leftarrow x^{(k)} - v$`

```r
x[1,] <- c(1,1)
gamma <- .2
eta <- .9
v <- c(0,0)
for (i in 2:40) {
  v <- eta * v + gamma * grad(x[i-1,] - gamma * v)
  x[i,] <- x[i-1,] - v
}
```

]

.pull-right[

<img src="rmd_gfx/04-gradient-descent/unnamed-chunk-16-1.svg" style="display: block; margin: auto;" />
]

---

## When do we stop?

For `$\epsilon>0$`, small

Check any/all of

1. `$\|f'(x)\| < \epsilon$`

2. `$\|x^{(k)} - x^{(k-1)}\| < \epsilon$`

3. `$\|f(x^{(k)}) - f(x^{(k-1)})\| < \epsilon$`

---

## Subgradient descent

What happens when `$f$` isn't differentiable?

A __subgradient__ of convex `$f$` at a point `$x$` is any `$g$` such that
`$$f(y) \geq f(x) + g^\top (y-x)\quad\quad \forall y$$`

- Always exists
- `$f$` differentiable `$\Rightarrow g=\nabla f(x)$` (unique)
- Just plug in the subgradient in GD
- `$f$` Lipschitz gives `$O(1/\sqrt{k})$` convergence

---

## Example (LASSO)

`$$\min_{\beta} \frac{1}{2n}\norm{y - X\beta}_2^2 + \lambda\norm{\beta}_1$$`

- Subdifferential (the set of subgradients)

`$$\begin{aligned}
g(\beta) &= -X^T(y - X\beta) + \lambda\partial\norm{\beta}_1 \\
& =-X^\top(y - X\beta) + \lambda v \\
v_i &=
    \begin{cases}
        \{1\}      & \quad \text{if } \beta_i > 0\\
        \{-1\}      & \quad \text{if } \beta_i < 0\\
        [-1,1]     & \quad \text{if } \beta_i = 0\\
    \end{cases}
\end{aligned}$$`

So `$\textrm{sign}(\beta) \in \partial\norm{\beta}_1$`