n <- 1000
set.seed(12345)
nseq <- 5
generate_ar <- function(id, n, b) {
y <- double(n)
y[1] <- rnorm(1)
for (i in 2:n) y[i] <- b * y[i - 1] + rnorm(1)
tibble(time = 1:n, y = y, id = id)
}
stationary <- map_dfr(1:nseq, ~ generate_ar(.x, n = n, b = .99))
non_stationary <- map_dfr(1:nseq, ~ generate_ar(.x, n = n, b = 1.01))Time series, a whirlwind
STAT 550
Daniel J. McDonald
The general linear process
- Imagine that there is a noise process
\[\epsilon_j \sim \textrm{N}(0, 1),\ \textrm{i.i.d.}\]
- At time \(i\), we observe the sum of all past noise
\[y_i = \sum_{j=-\infty}^0 a_{i+j} \epsilon_j\]
- Without some conditions on \(\{a_k\}_{k=-\infty}^0\) this process will “run away”
- The result is “non-stationary” and difficult to analyze.
- Stationary means (roughly) that the marginal distribution of \(y_i\) does not change with \(i\).
Chasing stationarity
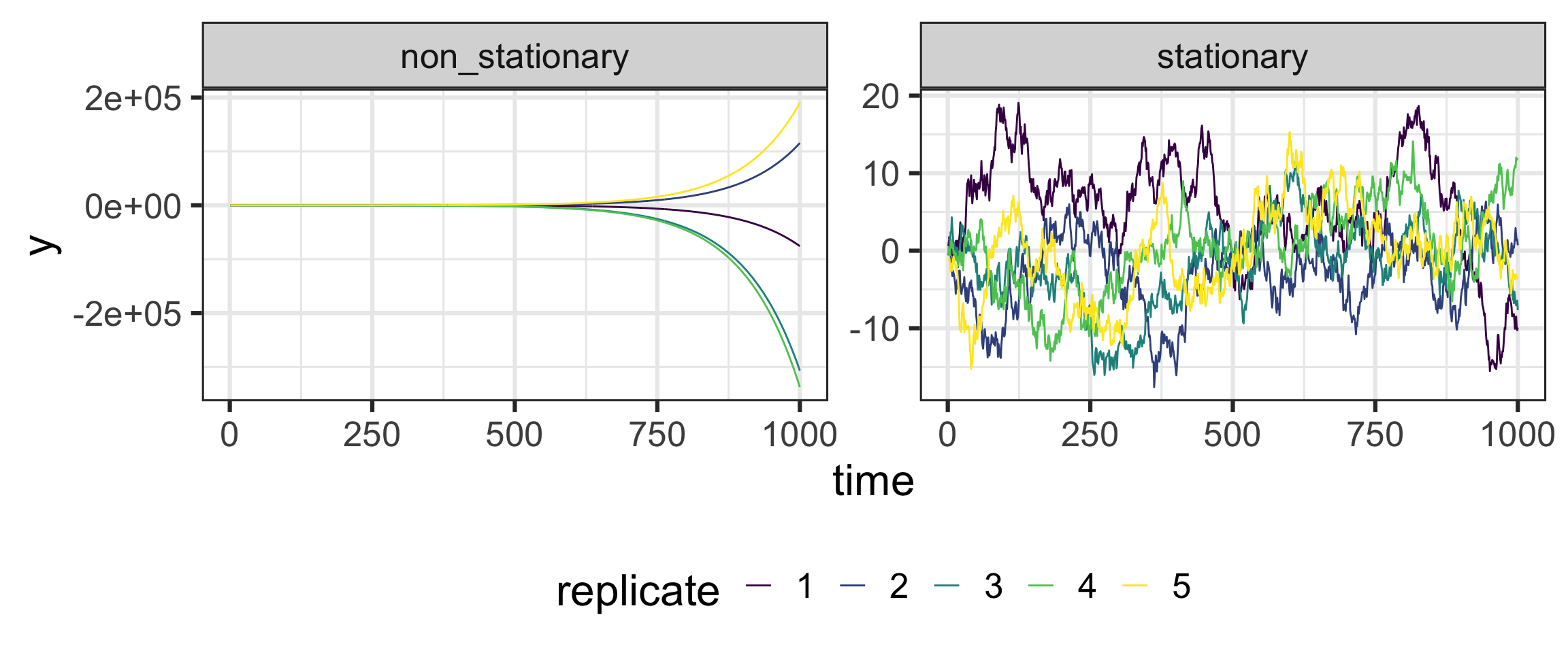
Uses of stationarity
- Lots of types (weak, strong, in-mean, wide-sense,…)
- not required for modelling / forecasting
- But assuming stationarity gives some important guarantees
- Usually work with stationary processes
Standard models
AR(p)
Suppose \(\epsilon_i\) are i.i.d. N(0, 1) (distn is convenient, but not required)
\[y_i = \mu + a_1 y_{i-1} + \cdots + a_p y_{i-p} + \epsilon_i\]
- This is a special case of the general linear process
- You can recursively substitute this defn into itself to get that equation
Easy to estimate the a’s given a realization.
y <- arima.sim(list(ar = c(.7, -.1)), n = 1000)
Y <- y[3:1000]
X <- cbind(lag1 = y[2:999], lag2 = y[1:998])
summary(lm(Y ~ X + 0))
Call:
lm(formula = Y ~ X + 0)
Residuals:
Min 1Q Median 3Q Max
-3.6164 -0.6638 0.0271 0.6456 3.8367
Coefficients:
Estimate Std. Error t value Pr(>|t|)
Xlag1 0.66931 0.03167 21.134 <2e-16 ***
Xlag2 -0.04856 0.03167 -1.533 0.126
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9899 on 996 degrees of freedom
Multiple R-squared: 0.4085, Adjusted R-squared: 0.4073
F-statistic: 344 on 2 and 996 DF, p-value: < 2.2e-16AR(p)
- The estimate isn’t that accurate because the residuals (not the \(\epsilon\)’s) are correlated.
- (Usually, you get
1/nconvergence, here you don’t.) - Also, this isn’t the MLE. The likelihood includes \(p(y_1)\), \(p(y_2 | y_1)\) which
lm()ignored. - The Std. Errors are unjustified.
- But that was easy to do.
- The correct way is
Call:
arima(x = y, order = c(2, 0, 0), include.mean = FALSE)
Coefficients:
ar1 ar2
0.6686 -0.0485
s.e. 0.0316 0.0316
sigma^2 estimated as 0.9765: log likelihood = -1407.34, aic = 2820.67- The resulting estimates and SEs are identical, AFAICS.
MA(q)
Start with the general linear process, but truncate the infinite sum.
\[y_i = \sum_{j=-q}^0 a_{i+j} \epsilon_j\]
- This is termed a “moving average” process.
- though \(a_0 + \cdots a_{-q}\) don’t sum to 1.
- Can’t write this easily as a
lm()
MA(q) as an AR(1) hidden process
Let \(X_j = [\epsilon_{j-1},\ \ldots,\ \epsilon_{j-q}]\) and write
\[ \begin{aligned} X_i &= \begin{bmatrix} a_{i-1} & a_{i-2} & \cdots & a_{i-q}\\ 1 & 0 & \cdots & 0\\ & & \ddots \\ 0 & 0 & \cdots & 1\end{bmatrix} X_{i-1} + \begin{bmatrix} a_{i}\\ 0 \\ \vdots \\ 0 \end{bmatrix} \epsilon_i\\ y_i &= \begin{bmatrix} 1 & 0 & \cdots 0 \end{bmatrix} X_i \end{aligned} \]
- Now \(X\) is a \(q\)-dimensional AR(1) (but we don’t see it)
- \(y\) is deterministic conditional on \(X\)
- This is the usual way these are estimated using a State-Space Model
- Many time series models have multiple equivalent representations
ARIMA
- We’ve been using
arima()andarima.sim(), so what is left? - The “I” means “integrated”
- If, for example, we can write \(z_i = y_i - y_{i-1}\) and \(z\) follows an ARMA(p, q), we say \(y\) follows an ARIMA(p, 1, q).
- The middle term is the degree of differencing
Other standard models
Suppose we can write
\[ y_i = T_i + S_i + W_i \]
This is the “classical” decomposition of \(y\) into a Trend + Seasonal + Noise.
You can estimate this with a “Basic Structural Time Series Model” using StrucTS().
A related, though slightly different model is called the STL decomposition, estimated with stl().
This is “Seasonal Decomposition of Time Series by Loess”
(LOESS is “locally estimated scatterplot smoothing” named/proposed independently by Bill Cleveland though originally proposed about 15 years earlier and called the Savitsky-Golay Filter)
Quick example
sts <- StructTS(AirPassengers)
bc <- stl(AirPassengers, "periodic") # use sin/cos to represent the seasonal
tibble(time = seq(as.Date("1949-01-01"), as.Date("1960-12-31"), by = "month"),
AP = AirPassengers, StrucTS = fitted(sts)[,1], STL = rowSums(bc$time.series[,1:2])) %>%
pivot_longer(-time) %>%
ggplot(aes(time, value, color = name)) +
geom_line() +
theme_bw(base_size = 24) +
scale_color_viridis_d(name = "") +
theme(legend.position = "bottom")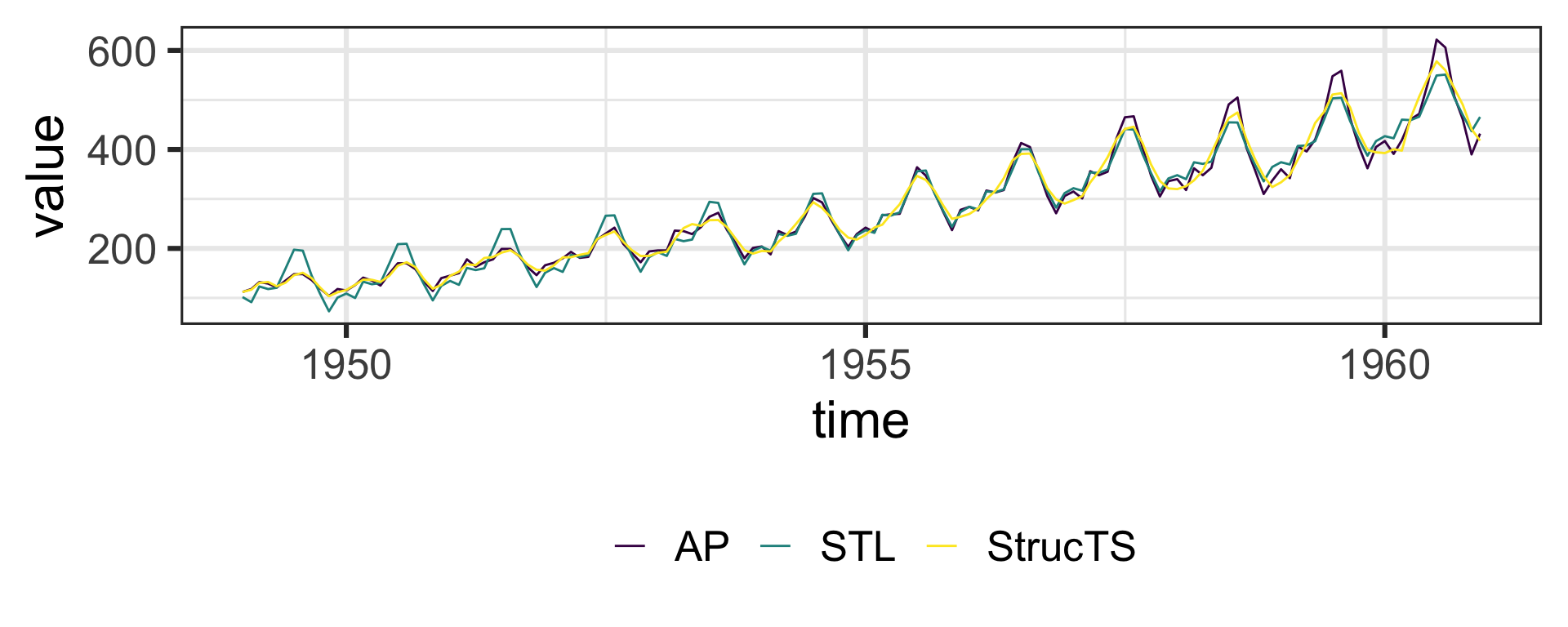
Generic state space model
\[\begin{aligned} x_k &\sim p(x_k | x_{k-1}) \\ y_k &\sim p(y_k | x_k)\end{aligned}\]
\(x_k\) is unobserved, dimension \(n\)
\(y_k\) is observed, dimension \(m\)
\(x\) process is the transition or process equation
\(y\) is the observation or measurement equation
Both are probability distributions that can depend on parameters \(\theta\)
For now, assume \(\theta\) is KNOWN
We can allow the densities to vary with time.
GOAL(s)
Filtering: given observations, find \[p(x_k | y_1,\ldots y_k)\]
Smoothing: given observations, find \[p(x_k | y_1,\ldots y_T), \;\;\ k < T\]
Forecasting: given observations, find \[p(y_{k+1} | y_1,\ldots,y_k)\]
Using Bayes Rule
Assume \(p(x_0)\) is known
\[ \begin{aligned} p(y_1,\ldots,y_T\ |\ x_1, \ldots, x_T) &= \prod_{k=1}^T p(y_k | x_k)\\ p(x_0,\ldots,x_T) &= p(x_0) \prod_{k=1}^T p(x_k | x_{k-1})\\ p(x_0,\ldots,x_T\ |\ y_1,\ldots,y_T) &= \frac{p(y_1,\ldots,y_T\ |\ x_1, \ldots, x_T)p(x_0,\ldots,x_T)}{p(y_1,\ldots,y_T)}\\ &\propto p(y_1,\ldots,y_T\ |\ x_1, \ldots, x_T)p(x_0,\ldots,x_T)\end{aligned} \]
In principle, if things are nice, you can compute this posterior (thinking of \(x\) as unknown parameters)
But in practice, computing a big multivariate posterior like this is computationally ill-advised.
Generic filtering
Recursively build up \(p(x_k | y_1,\ldots y_k)\).
Why? Because if we’re collecting data in real time, this is all we need to make forecasts for future data.
\[\begin{aligned} &p(y_{T+1} | y_1,\ldots,y_T)\\ &= p(y_{T+1} | x_{T+1}, y_1,\ldots,y_T)\\ &= p(y_{T+1} | x_{T+1} )p(x_{T+1} | y_1,\ldots,y_T)\\ &= p(y_{T+1} | x_{T+1} )p(x_{T+1} | x_T) p(x_T | y_1,\ldots,y_T)\end{aligned}\]
- Can continue to iterate if I want to predict \(h\) steps ahead
\[\begin{aligned} &p(y_{T+h} | y_1,\ldots,y_T)= p(y_{T+h} | x_{T+h} )\prod_{j=0}^{h-1} p(x_{T+j+1} | x_{T+j}) p(x_T | y_1,\ldots,y_T)\end{aligned}\]
The filtering recursion
- Initialization. Fix \(p(x_0)\).
Iterate the following for \(k=1,\ldots,T\):
Predict. \[p(x_k | y_{k-1}) = \int p(x_k | x_{k-1}) p(x_{k-1} | y_1,\ldots, y_{k-1})dx_{k-1}.\]
Update. \[p(x_k | y_1,\ldots,y_k) = \frac{p(y_k | x_k)p(x_k | y_1,\ldots,y_{k-1})}{p(y_1,\ldots,y_k)}\]
In general, this is somewhat annoying because these integrals may be challenging to solve.
But with some creativity, we can use Monte Carlo for everything.
What if we make lots of assumptions?
Assume that \[\begin{aligned}p(x_0) &= N(m_0, P_0) \\ p_k(x_k\ |\ x_{k-1}) &= N(A_{k-1}x_{k-1},\ Q_{k-1})\\ p_k(y_k\ |\ x_k) &= N(H_k x_k,\ R_k)\end{aligned}.\]
Then all the ugly integrals have closed-form representations by properties of conditional Gaussian distributions.
Closed-form representations
Distributions:
\[ \begin{aligned} p(x_k | y_1,\ldots,y_{k-1}) &= N(m^{-}_k, P^{-}_k)\\ p(x_k | y_1,\ldots,y_{k}) &= N(m_k, P_k)\\ p(y_{k} | y_1,\ldots,y_{k-1}) &= N(H_k m^-_k, S_k)\\ \end{aligned} \] Prediction: \[ \begin{aligned} m^-_k &= A_{k-1}m_{k-1}\\ P^-_k &= A_{k-1}P_{k-1}A^\mathsf{T}_{k-1} + Q_{k-1} \end{aligned} \]
Update: \[ \begin{aligned} v_k &= y_k - H_k m_k^-\\ S_k &= H_k P_k^- H_k^\mathsf{T} + R_k\\ K_k &= P^-_k H_k^\mathsf{T} S_k^{-1}\\ m_k &= m^-_k + K_{k}v_{k}\\ P_k &= P^-_k - K_k S_k K_k^\mathsf{T} \end{aligned} \]
Code or it isn’t real (Kalman Filter)
kalman <- function(y, m0, P0, A, Q, H, R) {
n <- length(y)
m <- double(n+1)
P <- double(n+1)
m[1] <- m0
P[1] <- P0
for (k in seq(n)) {
mm <- A * m[k]
Pm <- A * P[k] * A + Q
v <- y[k] - H * mm
S <- H * Pm * H + R
K <- Pm * H / S
m[k+1] <- mm + K * v
P[k+1] <- Pm - K * S * K
}
tibble(t = 1:n, m = m[-1], P = P[-1])
}
set.seed(2022-06-01)
x <- double(100)
for (k in 2:100) x[k] = x[k - 1] + rnorm(1)
y <- x + rnorm(100, sd = 1)
kf <- kalman(y, 0, 5, 1, 1, 1, 1)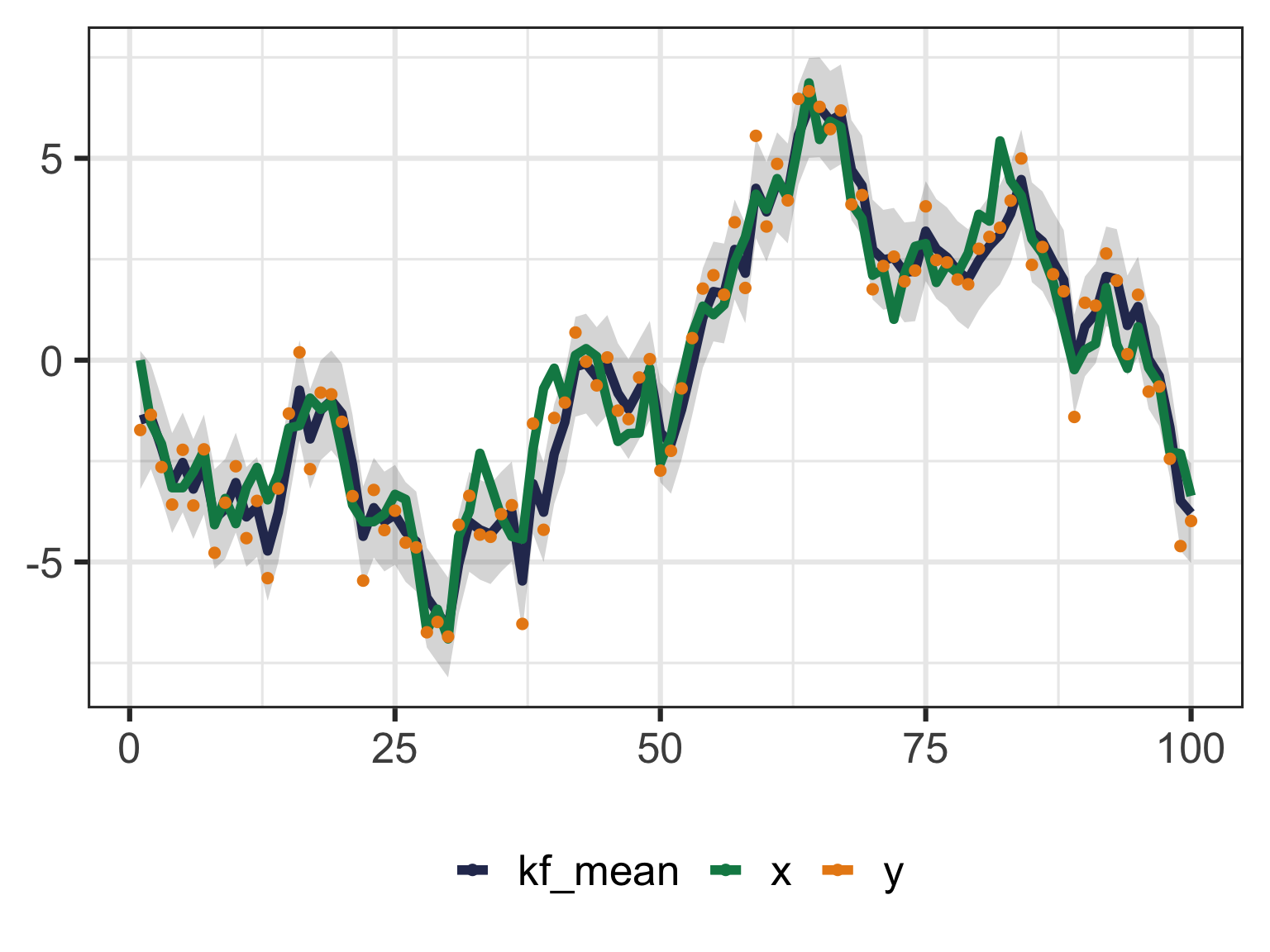
Important notes
- So far, we assumed all parameters were known.
- In reality, we had 6:
m0, P0, A, Q, H, R - I sort of also think of
xas “parameters” in the Bayesian sense - By that I mean, “latent variables for which we have prior distributions”
- What if we want to estimate them?
Bayesian way: m0 and P0 are already the parameters of for the prior on x1. Put priors on the other 4.
Frequentist way: Just maximize the likelihood. Can technically take P0 \(\rightarrow\infty\) to remove it and m0
The Likelihood is produced as a by-product of the Kalman Filter.
\[-\ell(\theta) = \sum_{k=1}^T \left(v_k^\mathsf{T}S_k^{-1}v_k + \log |S_k| + m \log 2\pi\right)\]
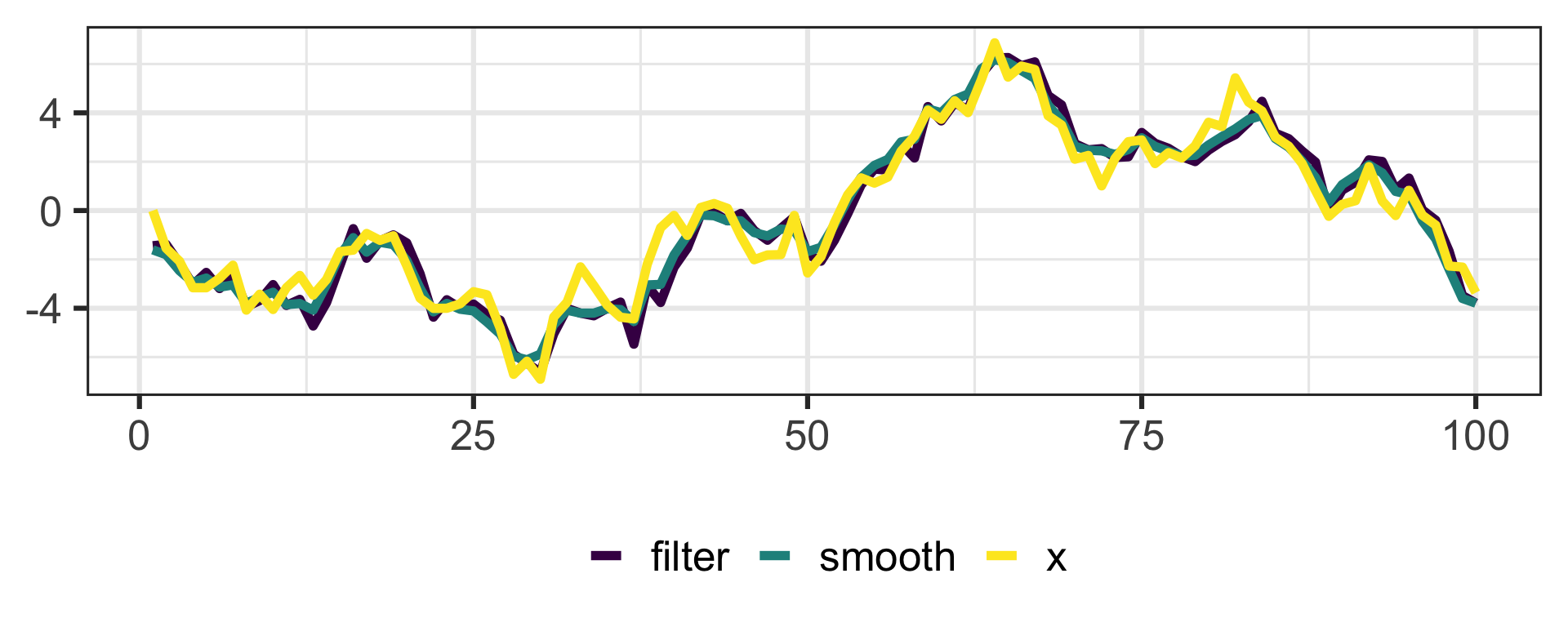
Smoothing
- We also want \(p(x_k | y_1,\ldots,y_{T})\)
- Filtering went “forward” in time. At the end we got, \(p(x_T | y_1,\ldots,y_{T})\). Smoothing starts there and goes “backward”
- For “everything linear Gaussian”, this is again “easy”
- Set \(m_T^s = m_T\), \(P_T^s = P_T\).
- For \(k = T-1,\ldots,1\),
\[\begin{aligned} G_k &= P_k A_k^\mathsf{T} [P_{k+1}^-]^{-1}\\ m_k^s &= m_k + G_k(m_{k+1}^s - m_{k+1}^-)\\ P_k^s &= P_k + G_k(P_{k+1}^s - P_{k+1}^-)G_k^\mathsf{T}\\ x_k | y_1,\ldots,y_T &= N(m^s_k, P_k^s) \end{aligned}\]
Comparing the filter and the smoother
- Same data, different code (using a package)
What about non-linear and/or non-Gaussian
\[\begin{aligned} x_k &\sim p(x_k | x_{k-1}) \\ y_k &\sim p(y_k | x_k)\end{aligned}\]
Then we need to solve integrals. This is a pain. We approximate them.
These all give approximations to the filtering distribution
- Extended Kalman filter - basically do a Taylor approximation, then do Kalman like
- Uncented Kalman filter - Approximate integrals with Sigma points
- Particle filter - Sequential Monte Carlo
- Bootstrap filter (simple version of SMC)
- Laplace Gaussian filter - Do a Laplace approximation to the distributions
The bootstrap filter
- Need to simulate from the transition distribution (
rtrans) - Need to evaluate the observation distribution (
dobs)
boot_filter <-
function(y, B = 1000, rtrans, dobs, a0 = 0, P0 = 1, perturb = function(x) x) {
n <- length(y)
filter_est <- matrix(0, n, B)
predict_est <- matrix(0, n, B)
init <- rnorm(B, a0, P0)
filter_est[1, ] = init
for (i in seq(n)) {
raw_w <- dobs(y[i], filter_est[i, ])
w <- raw_w / sum(raw_w)
selection <- sample.int(B, replace = TRUE, prob = w)
filter_est[i, ] <- perturb(filter_est[i, selection])
predict_est[i, ] <- rtrans(filter_est[i, ])
if (i < n) filter_est[i + 1, ] <- predict_est[i, ]
}
list(filt = filter_est, pred = predict_est)
}