Statistical models and model selection

Stat 550

Daniel J. McDonald

Last modified – 03 April 2024

\[ \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\minimize}{minimize} \DeclareMathOperator*{\maximize}{maximize} \DeclareMathOperator*{\find}{find} \DeclareMathOperator{\st}{subject\,\,to} \newcommand{\E}{E} \newcommand{\Expect}[1]{\E\left[ #1 \right]} \newcommand{\Var}[1]{\mathrm{Var}\left[ #1 \right]} \newcommand{\Cov}[2]{\mathrm{Cov}\left[#1,\ #2\right]} \newcommand{\given}{\mid} \newcommand{\X}{\mathbf{X}} \newcommand{\x}{\mathbf{x}} \newcommand{\y}{\mathbf{y}} \newcommand{\P}{\mathcal{P}} \newcommand{\R}{\mathbb{R}} \newcommand{\norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\snorm}[1]{\lVert #1 \rVert} \newcommand{\tr}[1]{\mbox{tr}(#1)} \newcommand{\U}{\mathbf{U}} \newcommand{\D}{\mathbf{D}} \newcommand{\V}{\mathbf{V}} \renewcommand{\hat}{\widehat} \]

What is a model?

In statistics, “model” has a mathematical meaning.

Distinct from “algorithm” or “procedure”.

Defining a model often leads to a procedure/algorithm with good properties.

Sometimes procedure/algorithm \(\Rightarrow\) a specific model.

Statistics (the field) tells me how to understand when different procedures are desirable and the mathematical guarantees that they satisfy.

When are certain models appropriate?

One definition of “Statistical Learning” is the “statistics behind the procedure”.

Statistical models 101

We observe data \(Z_1,\ Z_2,\ \ldots,\ Z_n\) generated by some probability distribution \(P\). We want to use the data to learn about \(P\).

A statistical model is a set of distributions \(\mathcal{P}\).

Some examples:

1. \(\P = \{ 0 < p < 1 : P(z=1)=p,\ P(z=0)=1-p\}\).
2. \(\P = \{ \beta \in \R^p,\ \sigma>0 : Y \sim N(X^\top\beta,\sigma^2),\ X\mbox{ fixed}\}\).
3. \(\P = \{\mbox{all CDF's }F\}\).
4. \(\P = \{\mbox{all smooth functions } f: \R^p \rightarrow \R : Z_i = (X_i, Y_i),\ E[Y_i] = f(X_i) \}\)

Statistical models

We want to use the data to select a distribution \(P\) that probably generated the data.

My model:

\[ \P = \{ P(z=1)=p,\ P(z=0)=1-p,\ 0 < p < 1 \} \]

• To completely characterize \(P\), I just need to estimate \(p\).

• Need to assume that \(P \in \P\).

• This assumption is mostly empty: need independent, can’t see \(z=12\).

Statistical models

We observe data \(Z_i=(Y_i,X_i)\) generated by some probability distribution \(P\). We want to use the data to learn about \(P\).

My model

\[ \P = \{ \beta \in \R^p, \sigma>0 : Y_i \given X_i=x_i \sim N(x_i^\top\beta,\ \sigma^2) \}. \]

• To completely characterize \(P\), I just need to estimate \(\beta\) and \(\sigma\).

• Need to assume that \(P\in\P\).

• This time, I have to assume a lot more: (conditional) Linearity, independence, conditional Gaussian noise, no ignored variables, no collinearity, etc.

Statistical models, unfamiliar example

We observe data \(Z_i \in \R\) generated by some probability distribution \(P\). We want to use the data to learn about \(P\).

My model

\[ \P = \{ Z_i \textrm{ has a density function } f \}. \]

• To completely characterize \(P\), I need to estimate \(f\).

• In fact, we can’t hope to do this.

Revised Model 1 - \(\P=\{ Z_i \textrm{ has a density function } f : \int (f'')^2 dx < M \}\)

Revised Model 2 - \(\P=\{ Z_i \textrm{ has a density function } f : \int (f'')^2 dx < K < M \}\)

Revised Model 3 - \(\P=\{ Z_i \textrm{ has a density function } f : \int |f'| dx < M \}\)

• Each of these suggests different ways of estimating \(f\)

Assumption Lean Regression

Imagine \(Z = (Y, \mathbf{X}) \sim P\) with \(Y \in \R\) and \(\mathbf{X} = (1, X_1, \ldots, X_p)^\top\).

We are interested in the conditional distribution \(P_{Y|\mathbf{X}}\)

Suppose we think that there is some function of interest which relates \(Y\) and \(X\).

Let’s call this function \(\mu(\mathbf{X})\) for the moment. How do we estimate \(\mu\)? What is \(\mu\)?

To make this precise, we

• Have a model \(\P\).
• Need to define a “good” functional \(\mu\).
• Let’s loosely define “good” as

Given a new (random) \(Z\), \(\mu(\mathbf{X})\) is “close” to \(Y\).

See Berk et al. Assumption Lean Regression.

Evaluating “close”

We need more functions.

Choose some loss function \(\ell\) that measures how close \(\mu\) and \(Y\) are.

• Squared-error:
  \(\ell(y,\ \mu) = (y-\mu)^2\)

• Absolute-error:
  \(\ell(y,\ \mu) = |y-\mu|\)

• Zero-One:
  \(\ell(y,\ \mu) = I(y\neq\mu)=\begin{cases} 0 & y=\mu\\1 & \mbox{else}\end{cases}\)

• Cauchy:
  \(\ell(y,\ \mu) = \log(1 + (y - \mu)^2)\)

Start with (Expected) Squared Error

Let’s try to minimize the expected squared error (MSE).

Claim: \(\mu(X) = \Expect{Y\ \vert\ X}\) minimizes MSE.

That is, for any \(r(X)\), \(\Expect{(Y - \mu(X))^2} \leq \Expect{(Y-r(X))^2}\).

Proof of Claim:

\[\begin{aligned} \Expect{(Y-r(X))^2} &= \Expect{(Y- \mu(X) + \mu(X) - r(X))^2}\\ &= \Expect{(Y- \mu(X))^2} + \Expect{(\mu(X) - r(X))^2} \\ &\quad +2\Expect{(Y- \mu(X))(\mu(X) - r(X))}\\ &=\Expect{(Y- \mu(X))^2} + \Expect{(\mu(X) - r(X))^2} \\ &\quad +2(\mu(X) - r(X))\Expect{(Y- \mu(X))}\\ &=\Expect{(Y- \mu(X))^2} + \Expect{(\mu(X) - r(X))^2} + 0\\ &\geq \Expect{(Y- \mu(X))^2} \end{aligned}\]

The regression function

Sometimes people call this solution:

\[\mu(X) = \Expect{Y \ \vert\ X}\]

the regression function. (But don’t forget that it depended on \(\ell\).)

If we assume that \(\mu(x) = \Expect{Y \ \vert\ X=x} = x^\top \beta\), then we get back exactly OLS.

But why should we assume \(\mu(x) = x^\top \beta\)?

Brief aside

Some notation / terminology

• “Hats” on things mean “estimates”, so \(\widehat{\mu}\) is an estimate of \(\mu\)

• Parameters are “properties of the model”, so \(f_X(x)\) or \(\mu\) or \(\Var{Y}\)

• Random variables like \(X\), \(Y\), \(Z\) may eventually become data, \(x\), \(y\), \(z\), once observed.

• “Estimating” means “using observations to estimate parameters”

• “Predicting” means “using observations to predict future data”

• Often, there is a parameter whose estimate will provide a prediction.

• “Non-parametric” means “we don’t assume a parametric form” for the regression function (or density)

Estimation vs. Prediction

• In consulting, you’re usually interested in estimating parameters accurately.

• This is a departure from machine learning, when you want to predict new data.

• But to “select a model”, we may have to choose between plausible alternatives.

• This can be challenging to understand.

Prediction risk for regression

Given the training data \(\mathcal{D}\), we want to predict some independent test data \(Z = (X,Y)\)

This means forming a \(\hat f\), which is a function of both the range of \(X\) and the training data \(\mathcal{D}\), which provides predictions \(\hat Y = \hat f(X)\).

The quality of this prediction is measured via the prediction risk \[R(\hat{f}) = \Expect{(Y - \hat{f}(X))^2}.\]

We know that the regression function, \(\mu(X) = \mathbb{E}[Y \mid X]\), is the best possible predictor.

Model selection and tuning parameters

• Often “model selection” means “choosing a set of predictors/variables”
  • E.g. Lasso performs model selection by setting many \(\widehat\beta=0\)
• “Model selection” really means > making any necessary decisions to arrive at a final model
• Sometimes this means “choosing predictors”
• It could also mean “selecting a tuning parameter”
• Or “deciding whether to use LASSO or Ridge” (and picking tuning parameters)
• Model selection means “choose \(\mathcal{P}\)”

My pet peeve

• Often people talk about “using LASSO” or “using an SVM”
• This isn’t quite right.
• LASSO is a regularized procedure that depends on \(\lambda\)
• To “use LASSO”, you must pick a particular \(\lambda\)
• Different ways to pick \(\lambda\) (today’s topic) produce different final estimators
• Thus we should say “I used LASSO + CV” or “I used Ridge + GCV”
• Probably also indicate “how” (I used the CV minimum.)

Bias and variance

Recall that \(\mathcal{D}\) is the training data.

\[R_n(f) := \Expect{L(Y,f(X))} = \Expect{\Expect{L(Y,f(X)) \given \mathcal{D}}}\]

• Note the difference between \(R_n(f)\;\;\textrm{and}\;\;\Expect{L(Y,f(X)) \given \mathcal{D}}\)
• If you use \(\mathcal{D}\) to choose \(f\), then these are different.
• If you use \(\mathcal{D}\) to choose \(f\), then both depend on how much data you have seen.

Risk estimates

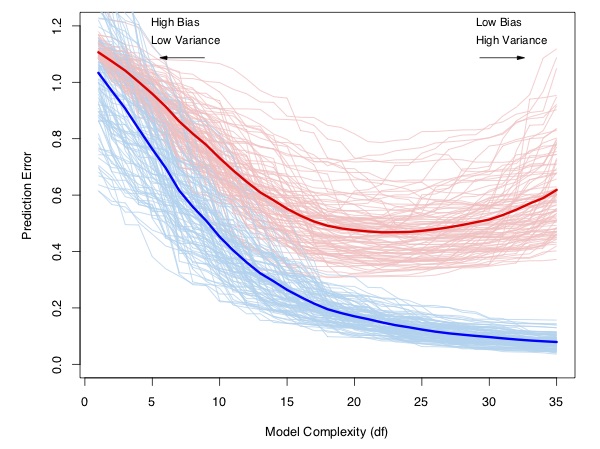
(Hastie, Tibshirani, and Friedman 2009)

• We can use risk estimates for 2 different goals

1. Choosing between different potential models.
2. Characterizing the out-of-sample performance of the chosen model.

• I am not generally aware of other methods of accomplishing (1).

A model selection picture

(Hastie, Tibshirani, and Friedman 2009)

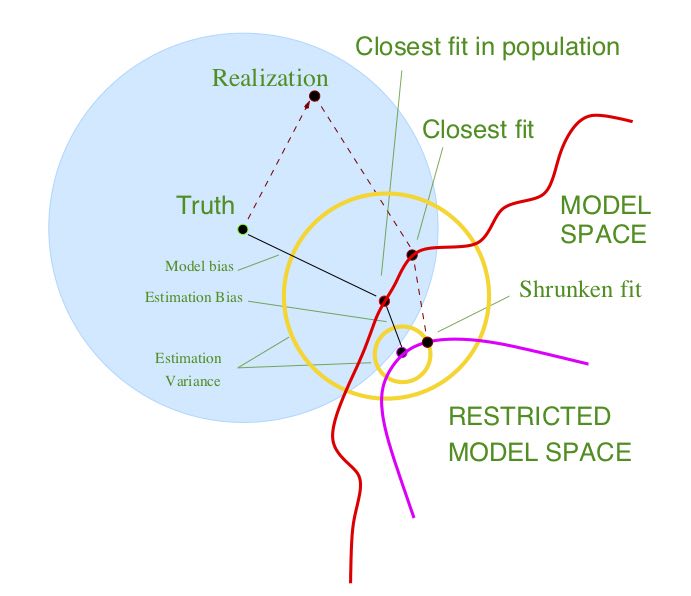
Why?

We want to do model selection for at least three reasons:

Prediction accuracy

Can essentially always be improved by introducing some bias

Interpretation

A large number of features can sometimes be reduced to an interpretable subset

Computation

A large \(p\) can create a huge computational bottleneck.

Things you shouldn’t do

• Estimate \(R_n\) with \(\widehat{R}_n(f) = \sum_{i=1}^n L(Y_i,\widehat{f}(X_i))\).
• Throw away variables with small \(p\)-values.
• Use \(F\)-tests
• Compare the log-likelihood between different models

These last two can occasionally be ok, but aren’t in general. You should investigate the assumptions that are implicit in them.

Risk estimators

Unbiased risk estimation

• It is very hard (impossible?) to estimate \(R_n\).
• Instead we focus on

\[\overline{R}_n(f) = \E_{Y_1,\ldots,Y_n}\left[\E_{Y^0}\left[\frac{1}{n}\sum_{i=1}^n L(Y^0_i,\hat{f}(x_i))\given \mathcal{D}\right]\right].\]

• The difference is that \(\overline{R}_n(f)\) averages over the observed \(x_i\) rather than taking the expected value over the distribution of \(X\).
• In the “fixed design” setting, these are equal.

Unbiased risk estimation

For many \(L\) and some predictor \(\hat{f}\), one can show

\[\overline{R}_n(\hat{f}) = \Expect{\hat{R}_n(\hat{f})} + \frac{2}{n} \sum_{i=1}^n \Cov{Y_i}{\hat{f}(x_i)}.\]

This suggests estimating \(\overline{R}_n(\hat{f})\) with

\[\hat{R}_{\textrm{gic}} := \hat{R}_n(\hat{f}) + \textrm{pen}.\]

If \(\Expect{\textrm{pen}} = \frac{2}{n}\sum_{i=1}^n \Cov{Y_i}{\hat{f}(x_i)}\), we have an unbiased estimator of \(\overline{R}_n(\hat{f})\).

Normal means model

Suppose we observe the following data:

\[Y_i = \beta_i + \epsilon_i, \quad\quad i=1,\ldots,n\]

where \(\epsilon_i\overset{iid}{\sim} \mbox{N}(0,1)\).

We want to estimate \[\boldsymbol{\beta} = (\beta_1,\ldots,\beta_n).\]

The usual estimator (MLE) is \[\widehat{\boldsymbol{\beta}}^{MLE} = (Y_1,\ldots,Y_n).\]

This estimator has lots of nice properties: consistent, unbiased, UMVUE, (asymptotic) normality…

MLEs are bad

But, the standard estimator STINKS! It’s a bad estimator.

It has no bias, but big variance.

\[R_n(\widehat{\boldsymbol{\beta}}^{MLE}) = \mbox{bias}^2 + \mbox{var} = 0 + n\cdot 1= n\]

What if we use a biased estimator?

Consider the following estimator instead: \[\widehat{\beta}_i^S = \begin{cases} Y_i & i \in S\\ 0 & \mbox{else}. \end{cases}\]

Here \(S \subseteq \{1,\ldots,n\}\).

Biased normal means

What is the risk of this estimator?

\[ R_n(\widehat{\boldsymbol{\beta}}^S) = \sum_{i\not\in S} \beta_i^2 + |S|. \]

In other words, if some \(|\beta_i| < 1\), then don’t bother estimating them!

In general, introduced parameters like \(S\) will be called tuning parameters.

Of course we don’t know which \(|\beta_i| < 1\).

But we could try to estimate \(R_n(\widehat{\boldsymbol{\beta}}^S)\), and choose \(S\) to minimize our estimate.

Dangers of using the training error

Although

\[\widehat{R}_n(\widehat{\boldsymbol{\beta}}) \approx R_n(\widehat{\boldsymbol{\beta}}),\] this approximation can be very bad. In fact:

Training Error

\(\widehat{R}_n(\widehat{\boldsymbol{\beta}}^{MLE}) = 0\)

Risk

\(R_n(\widehat{\boldsymbol{\beta}}^{MLE}) = n\)

In this case, the optimism of the training error is \(n\).

Normal means

What about \(\widehat{\boldsymbol{\beta}}^S\)?

\[\widehat{R}_n(\widehat{\boldsymbol{\beta}}^S) = \sum_{i=1}^n (\widehat{\beta_i}- Y_i)^2 = \sum_{i \notin S} Y_i^2 %+ |S|\sigma^2\]

Well \[\E\left[\widehat{R}_n(\widehat{\boldsymbol{\beta}}^S)\right] = R_n(\widehat{\boldsymbol{\beta}}^S) - 2|S| +n.\]

So I can choose \(S\) by minimizing \(\widehat{R}_n(\widehat{\boldsymbol{\beta}}^S) + 2|S|\).

\[\mbox{Estimate of Risk} = \mbox{training error} + \mbox{penalty}.\]

The penalty term corrects for the optimism.

pen() in the nice cases

Result:
Suppose \(\hat{f}(x_i) = HY\) for some matrix \(H\), and \(Y_i\)’s are IID. Then

\[\frac{2}{n} \sum_{i=1}^n \Cov{Y_i}{\hat{f}(x_i)} = \frac{2}{n} \sum_{i=1}^n H_{ii} \Cov{Y_i}{Y_i} = \frac{2\Var{Y}}{n} \tr{H}.\]

• Such estimators are called “linear smoothers”.
• Obvious extension to the heteroskedastic case.
• We call \(\frac{1}{\Var{Y}}\sum_{i=1}^n \Cov{Y_i}{\hat{f}(x_i)}\) the degrees of freedom of \(\hat{f}\).
• Linear smoothers are ubiquitous
• Examples: OLS, ridge regression, KNN, dictionary regression, smoothing splines, kernel regression, etc.

Examples of DF

• OLS

\[H = X^\top (X^\top X)^{-1} X^\top \Rightarrow \tr{H} = \textrm{rank}(X) = p\]

• Ridge (decompose \(X=UDV^\top\))

\[H = X^\top (X^\top X + \lambda I_p)^{-1} X^\top \Rightarrow \tr{H} = \sum_{i=1}^p \frac{d_i^2}{d_i^2 + \lambda} < \min\{p,n\}\]

• KNN \(\textrm{df} = n/K\) (each point is it’s own nearest neighbor, it gets weight \(1/K\))

Finding risk estimators

This isn’t the way everyone introduces/conceptualizes prediction risk.

For me, thinking of \(\hat{R}_n\) as overly optimistic and correcting for that optimism is conceptually appealing

An alternative approach is to discuss information criteria.

In this case one forms a (pseudo)-metric on probability measures.

Comparing probability measures

Kullback–Leibler

Suppose we have data \(Y\) that comes from the probability density function \(f\).

What happens if we use the probability density function \(g\) instead?

Example

Suppose \(Y \sim N(\mu,\sigma^2) =: f\). We want to predict a new \(Y_*\), but we model it as \(Y_* \sim N(\mu_*,\sigma^2) =: g\)

How far away are we? We can either compare \(\mu\) to \(\mu_*\) or \(Y\) to \(Y^*\).

Or, we can compute how far \(f\) is from \(g\).

We need a notion of distance.

Kullback–Leibler

Kullback–Leibler divergence (or discrepancy)

\[\begin{aligned} KL(f\;\Vert\; g) & = \int \log\left( \frac{f(y)}{g(y)} \right)f(y) dy \\ & \propto -\int \log (g(y)) f(y) dy \qquad \textrm{(ignore term without $g$)}\\ & = -\mathbb{E}_f [\log (g(Y))] \end{aligned}\]

• Measures the loss incurred by (incorrectly) using \(g\) instead of \(f\).

• KL is not symmetric: \(KL(f\;\Vert\; g) \neq KL(g\;\Vert\; f)\), so it’s not a distance, but it is non-negative and satisfies the triangle inequality.

• Usually, \(f,\ g\) will depend on some parameters, call them \(\theta\)

KL example

• In regression, we can specify \(f = N(X^{\top} \beta_*, \sigma^2)\)
• for a fixed (true) \(\beta_*\),
• let \(g_\theta = N(X^{\top}\beta,\sigma^2)\) over all \(\theta = (\beta,\sigma^2) \in \mathbb{R}^p\times\mathbb{R}^+\)
• \(KL(f,g_\theta) = -\mathbb{E}_f [\log (g_\theta(Y))]\), we want to minimize this over \(\theta\).
• But \(f\) is unknown, so we minimize \(-\log (g_\theta(Y))\) instead.
• This is the maximum likelihood value \[\hat{\theta}_{ML} = \argmax_\theta g_\theta(Y)\]
• We don’t actually need to assume things about a true model nor have it be nested in the alternative models to make this work.

Operationalizing

• Now, to get an operational characterization of the KL divergence at the ML solution \[-\mathbb{E}_f [\log (g_{\hat\theta_{ML}}(Y))]\] we need an approximation (don’t know \(f\), still).

Result

If you maximize the likelihood for a finite dimensional parameter vector \(\theta\) of length \(p\), then as \(n\rightarrow \infty\), \[-\mathbb{E}_f [\log (g_{\hat\theta_{ML}}(Y))] = -\log (g_{\hat\theta_{ML}}(Y)) + p.\]

• This is AIC (originally “an information criterion”, now “Akaike’s information criterion”).

AIC warnings

• Choose the model with smallest AIC
• Often multiplied by 2 “for historical reasons”.
• Sometimes by \(-2\) “to be extra annoying”.
• Your estimator for \(\theta\) needs to be the MLE. (or the asymptotics may be wrong)
• \(p\) includes all estimated parameters.

Back to the OLS example

Suppose \(Y\) comes from the standard normal linear regression model with known variance \(\sigma^2\).

\[ \begin{aligned} -\log(g_{\hat{\theta}}) &\propto \log(\sigma^2) + \frac{1}{2\sigma^2}\sum_{i=1}^n (y_i - x_i^\top \hat{\beta}_{MLE})^2\\ \Rightarrow AIC &= 2\frac{n}{2\sigma^2}\hat{R}_n + 2p = \hat{R}_n + \frac{2\sigma^2}{n} p. \end{aligned} \]

Back to the OLS example

Suppose \(Y\) comes from the standard normal linear regression model with unknown variance \(\sigma^2\).

Note that \(\hat{\sigma}_{MLE}^2 = \frac{1}{n} \sum_{i=1}^n (y_i-x_i^\top\hat{\beta}_{MLE})^2\).

\[ \begin{aligned} -\log(g_{\hat{\theta}}) &\propto \frac{n}{2}\log(\hat{\sigma}^2) + \frac{1}{2\hat{\sigma^2}}\sum_{i=1}^n (y_i - x_i^\top \hat{\beta}_{MLE})^2\\ \Rightarrow AIC &\propto 2 n\log(\hat{\sigma}^2)/2 + 2(p+1) \propto \log(\hat{R}_n) + \frac{2(p+1)}{n}. \end{aligned} \]

Mallow’s Cp

• Defined for linear regression.
• No likelihood assumptions.
• Variance is known

\[C_p = \hat{R}_n + 2\sigma^2 \frac{\textrm{df}}{n} = AIC\]

Bayes factor

For Bayesian Analysis, we want the posterior. Suppose we have two models A and B.

\[ \begin{aligned} P(B\given \mathcal{D}) &= \frac{P(\mathcal{D}\given B)P(B)}{P(\mathcal{D})} \propto P(\mathcal{D}\given B)P(B)\\ P(A\given \mathcal{D}) &= \frac{P(\mathcal{D}\given A)P(A)}{P(\mathcal{D})} \propto P(\mathcal{D}\given A)P(A) \end{aligned} \] We assume that \(P(A) = P(B)\). Then to compare, \[ \frac{P(B\given \mathcal{D})}{P(A\given \mathcal{D})} = \frac{P(\mathcal{D}\given B)} {P(\mathcal{D}\given A)}. \]

• Called the Bayes Factor.
• This is the ratio of marginal likelihoods under the different models.

Bayes Factor

• Not easy to calculate generally. ()
• Use the Laplace approximation, some simplifications, assumptions:

\[\log P(\mathcal{D}\given B) = \log P(\mathcal{D} \given \hat{\theta},\ B) -\frac{p\log(n)}{2} + O(1) \]

• Multiply through by \(-2\): \[ BIC = -\log (g_\theta(Y)) + p\log(n) = \log(\hat{R}_n) + \frac{p\log(n)}{n} \]

• Also called Schwarz IC. Compare to AIC (variance unknown case)

SURE

\[\hat{R}_{gic} := \hat{R}_n(\hat{f}) + \textrm{pen}.\]

If \(\Expect{\textrm{pen}} = \frac{2}{n}\sum_{i=1}^n \Cov{Y_i}{\hat{f}(x_i)}\), we have an unbiased estimator of \(\overline{R}_n(\hat{f})\).

Result (Stein’s Lemma)

Suppose \(Y_i\sim N(\mu_i,\sigma^2)\) and suppose \(f\) is weakly differentiable. Then

\[\frac{1}{\sigma^2} \sum_{i=1}^n\Cov{Y_i}{\hat{f}_i(Y)} = \Expect{\sum_{i=1}^n \frac{\partial f_i}{\partial y_i} \hat{f}(Y)}.\]

• Note: Here I’m writing \(\hat{f}\) as a function of \(Y\) rather than \(x\).

SURE

• This gives “Stein’s Unbiased Risk Estimator”

\[SURE = \hat{R}_n(\hat{f}) + 2\sigma^2 \sum_{i=1}^n \frac{\partial f_i}{\partial y_i} \hat{f}(Y) - n\sigma^2.\]

• If \(f(Y) = HY\) is linear, we’re back to AIC (variance known case)

• If \(\sigma^2\) is unknown, may not be unbiased anymore. May not care.

CV

Intuition for CV

One reason that \(\widehat{R}_n(\widehat{f})\) is bad is that we are using the same data to pick \(\widehat{f}\) AND to estimate \(R_n\).

“Validation set” fixes this, but holds out a particular, fixed block of data we pretend mimics the “test data”

What if we set aside one observation, say the first one \((y_1, x_1)\).

We estimate \(\widehat{f}^{(1)}\) without using the first observation.

Then we test our prediction:

\[\widetilde{R}_1(\widehat{f}^{(1)}) = (y_1 -\widehat{f}^{(1)}(x_1))^2.\]

(why the notation \(\widetilde{R}_1\)? Because we’re estimating the risk with 1 observation. )

Keep going

But that was only one data point \((y_1, x_1)\). Why stop there?

Do the same with \((y_2, x_2)\)! Get an estimate \(\widehat{f}^{(2)}\) without using it, then

\[\widetilde{R}_1(\widehat{f}^{(2)}) = (y_2 -\widehat{f}^{(2)}(x_2))^2.\]

We can keep doing this until we try it for every data point.

And then average them! (Averages are good)

\[\mbox{LOO-CV} = \frac{1}{n}\sum_{i=1}^n \widetilde{R}_1(\widehat{f}^{(i)}) = \frac{1}{n}\sum_{i=1}^n (y_i - \widehat{f}^{(i)}(x_i))^2\]

This is leave-one-out cross validation

Problems with LOO-CV

🤮 Each held out set is small \((n=1)\). Therefore, the variance of the Squared Error of each prediction is high.

🤮 The training sets overlap. This is bad.

• Usually, averaging reduces variance: \(\Var{\overline{X}} = \frac{1}{n^2}\sum_{i=1}^n \Var{X_i} = \frac{1}{n}\Var{X_1}.\)
• But only if the variables are independent. If not, then \(\Var{\overline{X}} = \frac{1}{n^2}\Var{ \sum_{i=1}^n X_i} = \frac{1}{n}\Var{X_1} + \frac{1}{n^2}\sum_{i\neq j} \Cov{X_i}{X_j}.\)
• Since the training sets overlap a lot, that covariance can be pretty big.

🤮 We have to estimate this model \(n\) times.

🎉 Bias is low because we used almost all the data to fit the model: \(E[\mbox{LOO-CV}] = R_{n-1}\)

K-fold CV

To alleviate some of these problems, people usually use \(K\)-fold cross validation.

The idea of \(K\)-fold is

1. Divide the data into \(K\) groups.
2. Leave a group out and estimate with the rest.
3. Test on the held-out group. Calculate an average risk over these \(\sim n/K\) data.
4. Repeat for all \(K\) groups.
5. Average the average risks.

🎉 Less overlap, smaller covariance.

🎉 Larger hold-out sets, smaller variance.

🎉 Less computations (only need to estimate \(K\) times)

🤮 LOO-CV is (nearly) unbiased for \(R_n\)

🤮 K-fold CV is unbiased for \(R_{n(1-1/K)}\)

The risk depends on how much data you use to estimate the model. \(R_n\) depends on \(n\).

Comparison

• LOO-CV and AIC are asymptotically equivalent \(p<n\), (Stone 1977)
• Properties of AIC/BIC in high dimensions are not well understood.
• In low dimensions, AIC is minimax optimal for the prediction risk (Yang and Barron 1998)
• CV is consistent for the prediction risk (Dudoit and Laan 2005)
• Both tend to over-select predictors (unproven, except empirically)
• BIC asymptotically selects the correct linear model in low dimensions (Shao 1997) and in high dimensions (Wang, Li, and Leng 2009)

Comparison

• In linear regression, it is impossible for a model selection criterion to be minimax optimal and select the correct model asymptotically (Yang 2005)
• In high dimensions, if the variance is unknown, the “known” variance form of AIC/BIC is disastrous.
• Conclusion: your choice of risk estimator impacts results. Thus,
  1. If you want to select models, you might pick BIC
  2. If you want good predictions, you might use CV
  3. It’s possible LASSO + CV(1se) picks models better than LASSO + CV(min)

Some other lessons

• The unknown variance form of AIC fails in high dimensions because you can drive RSS to zero.
• You need to use a high-dimensional variance estimator instead (Homrighausen and McDonald 2018)
• LASSO + CV “works” in high dimensions (not LOO, but no one uses it anyway)
• Under very strong conditions it selects the right model at the right rate.
• Under weaker conditions, it achieves (nearly) minimax optimal prediction risk. (Homrighausen and McDonald 2013, 2014, 2017)

What if we don’t want to choose?

1. Choose a risk estimator \(\hat{R}\)
2. Calculate weights \(p_i = \exp\left\{-\hat{R}(\textrm{Model}_i)\right\}\)
3. Create final estimator \(\hat{f} = \sum_{\textrm{models}} \frac{p_i}{\sum p_i} \hat{f}_i\).

• If \(\hat{R}\) is BIC, this is (poor-man’s) Bayesian Model Averaging.

Bayesian Model Averaging

• Real BMA integrates over the models: \[P(f \given \mathcal{D}) = \int P(f \given M_i, \mathcal{D}) P(M_i \given \mathcal{D}) dM\]
• Averaging + Sparsity is pretty hard.
• Interesting open problem: how can we combine LASSO models over the path?
• Issue with MA: \(e^{-BIC}\) can be tiny for all but a few models. You’re not averaging anymore.

References

Dudoit, Sandrine, and Mark J. van der Laan. 2005. “Asymptotics of Cross-Validation Risk Estimation in Estimator Selection and Performance Assessment.” Statistical Methodology, 131–54.

Hastie, T., R. Tibshirani, and J. Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Verlag.

Homrighausen, Darren, and Daniel J. McDonald. 2013. “The Lasso, Persistence, and Cross-Validation.” In Proceedings of the \(30^{th}\) International Conference on Machine Learning (ICML), edited by Sanjoy Dasgupta and David McAllester, 28:1031–39. PMLR.

———. 2014. “Leave-One-Out Cross-Validation Is Risk Consistent for Lasso.” Machine Learning 97 (1-2): 65–78.

———. 2017. “Risk Consistency of Cross-Validation for Lasso-Type Procedures.” Statistica Sinica 27 (3): 1017–36.

———. 2018. “A Study on Tuning Parameter Selection for the High-Dimensional Lasso.” Journal of Statistical Computation and Simulation 88: 2865–92.

Shao, Jun. 1997. “An Asymptotic Theory for Linear Model Selection.” Statistica Sinica 7 (2): 221–42.

Stone, M. 1977. “Asymptotics for and Against Cross-Validation.” Biometrika 64 (1): 29–35.

Wang, Hansheng, Bo Li, and Chenlei Leng. 2009. “Shrinkage Tuning Parameter Selection with a Diverging Number of Parameters.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 71 (3): 671–83.

Yang, Yuhong. 2005. “Can the Strengths of AIC and BIC Be Shared? A Conflict Between Model Indentification and Regression Estimation.” Biometrika 92 (4): 937–50.

Yang, Yuhong, and Andrew Barron. 1998. “An Asymptotic Property of Model Selection Criteria.” IEEE Transactions on Information Theory 44: 95–116.